US States: Percent without Medical Insurance vs. Average Life Span

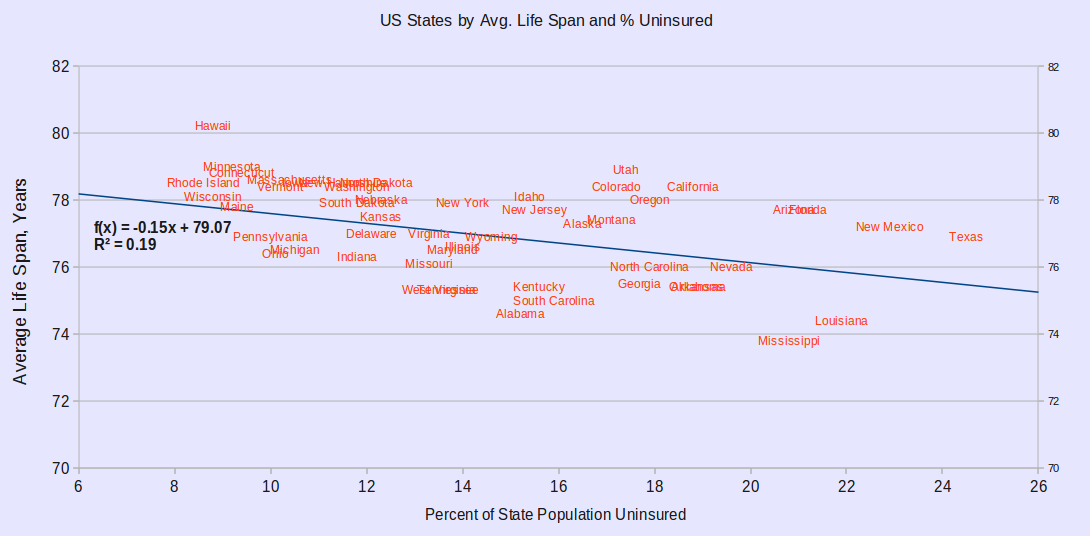
I found the average life spans of the 50 US states here:

http://www.top50states.com/life-expectancy.html

I found the % of population uninsured here:

http://www.aflcio.org/issues/healthcare/crisis.cfm

I put them together into a spreadsheet and graph here:

http://www.cuug.ab.ca/branderr/usamed

Since then, I've done two better graphs. The first shows the same points, but with the state names as labels:

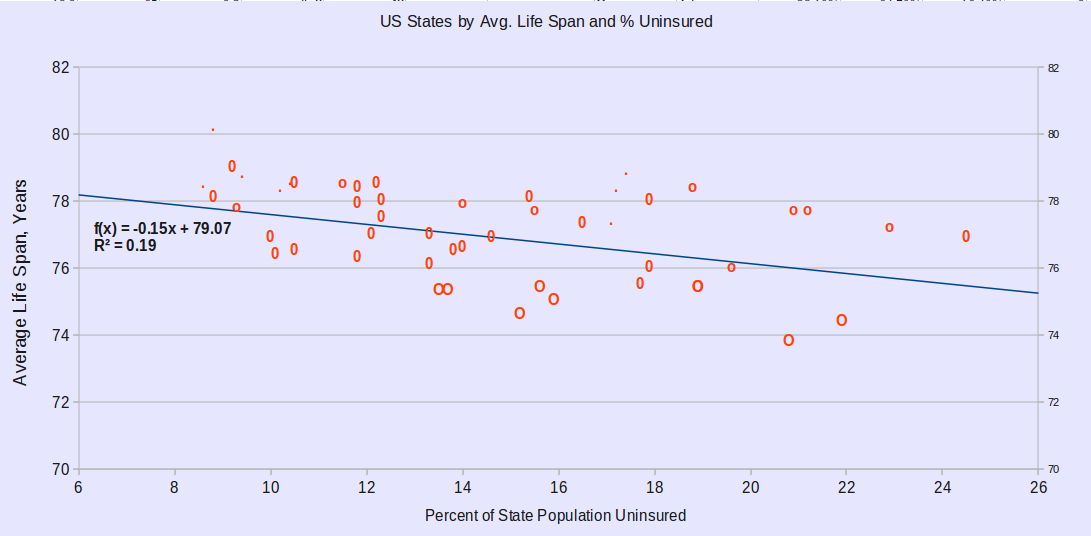
The second uses a dodge I came up with to show a third dimension. I found a list of the 50 States and their percent of obese adults, at: http://en.wikipedia.org/wiki/Obesity_in_the_United_States
I then used a spreadsheet formula to fill the "label" range not with state names, but with these characters:

% Obese Adults	Character
18-22	.
22-25	o
24-28	0
over28	O

That gives this graph:

The characters are larger with the higher percentage of obesity - think of them as average belt sizes viewed from above. You can see right off that some of the highest life spans above the trend line are the points, and most of the large "O" high-obesity states as the lowest below the trend line.

Is obesity or insurance the better correlation with lifespan? Let's graph the two against each other directly:

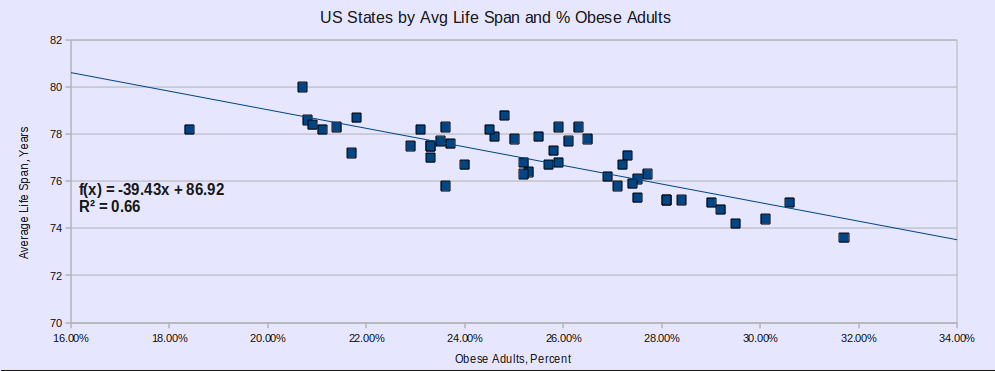
Yes! The dots cluster around the trendline much more closely. Indeed, the "r-squared" correlation coefficient has skyrocketed to 0.66 ! Obesity is a better predictor. But that doesn't mean that insurance isn't one, just a smaller one.

Long story short: this has all been done. It gets much harder to sort out multiple drivers of a result when there are several, and rather than my 33-year-old single stats course, which barely touched on the problem of multiple regression, you might want to be a PhD with several grad students or something. Perhaps at Harvard University, as noted by your True/Slant contributor Austin Considine. The Harvard Science Article that Austin links to in turn, notes that:

The study, which analyzed data from national surveys carried out by the Centers for Disease Control and Prevention (CDC), assessed death rates after taking into account education, income, and many other factors, including smoking, drinking, and obesity. It estimated that lack of health insurance causes 44,789 excess deaths annually.

"Average Life Span" is a function of the number of people who die at 45, at 46, at 47, and so on. Combine that with the demographic curve of the population, the number of people that ARE 45, 46, 47... and you have the yearly death rate.

I'm speaking in rather broad strokes compared to what I'm sure the Harvard study did. Especially to get the article accepted by the American Journal of Public Health, they would have been most sophisticated about their stats.

Working with their raw data, a much better estimate could be made of the contribution that lack of insurance makes to life span. Perhaps Harvard did so, if one reads the actual paper. But admit, it was much more dramatic, and just as correct, to state it in the news release as higher number of deaths per year.

Ms McArdle's article mentions these "observational studies". She apparently wrote this recently-published article before the September 17th, 2009 Harvard publication, because she doesn't mention it. (Or didn't understand that death-rate and life-span are so related, but I hope not that.) She notes that most of them are a little old, and casts doubts on the previous multiple regression "observational study" from the Institute of Medicine in 2002. That used similar methods, but had somewhat less data, taken from a "pioneering" 1993 study.

The contrary study that Ms McArdle spends some time on was done by Richard Kronick at UC San Diego. When I googled his name, I found a note from Jack Hadley and Timothy Waidmann at Health Services Research discussing his work and theirs, and the reconcilation between the two. They note that the effect of insurance is mostly on the health of the insured - they have better lives. Better generally means longer, but the number of "good years" may be more different than the number of total years.

Their first sentence notes that everybody is now only discussion how much insurance improves health, not whether it does; even Dr. Kronick is apparently on-board with that much; it's just the life span effect that he thinks is smaller than other researchers are concluding. To the extent that we should want health care that improves health while we live, even if it did not extend life's length, Ms. McArdle's article is a red herring. But, frankly, after looking over the Harvard press release, I'm still very inclined to believe they have something, and not that Dr. Kronick's work is some kind of debunking of a "Myth". It's another data-point among several.

I am not one of these researchers; neither I nor Ms. McArdle nor a battalion of bloggers are going to resolve the best estimate of insurance upon life span from many variant studies. What I do know, is that as a Canadian, I'm right off those graphs above: Canada, with its single-payer system, is at a national average of 80.7 years, better than Hawaii. Every developed country with universal insurance has longer life spans than the US, except for Portugal and Slovenia. So I'll just keep my single-payer while Ms McArdle figures it all out.

Spreadsheet in Excel XLS format

I can't guarantee the format of the Excel version, it was saved by Openoffice. The text and numbers will be fine, but the graph may suck. The image of it is above.

I did NOT verify the data. Both were quick grabs, the top links in a google search.

,